- Index
- Bienvenue sur le site WEB "industry-finder".
- Résolution du Conseil, du 7 mai 1985, concernant une nouvelle approche
- Nouveau guide bleu pour la mise en oeuvre des directives européennes pour les produits règles 2016
- l'éco-conception et les produits industriels
- le marquage CE des machines
- Le nouveau guide bleu daté de avril 2014
- Directive Machines
- Historique de la directive machines 2006/42/CE
- Directive machines 2006/42/CE
- Considerants de la directive machines 2006/42/CE
- Articles de la directive machines 2006/42/CE
- Article 1 de la directive machine 2006/42/CE - Champ d'application
- Article 2 de la directive machine 2006/42/CE - Definitions
- Article 3 de la directive machine 2006/42/CE - Directives particulières
- Article 4 de la directive machine 2006/42/CE - Surveillance du marché
- Article 5 de la directive machine 2006/42/CE - Mise sur le marché et mise en service
- Article 6 de la directive machine 2006/42/CE - Libre circulation
- Article 7 de la directive machine 2006/42/CE - Présomption de conformité et normes harmonisées
- Article 8 de la directive machine 2006/42/CE - Mesures spécifiques
- Article 9 de la directive machine 2006/42/CE - Mesures particulières visant des machines potentiellement dangereuses
- Article 10 de la directive machine 2006/42/CE - Procédure de contestation d'une norme harmonisée
- Article 11 de la directive machine 2006/42/CE - Clause de sauvegarde
- Article 12 : Procédures d'évaluation de la conformité des machines - directive machines 2006/42/CE
- Article 13 de la directive machine 2006/42/CE - Procédure pour les quasi-machines
- Article 14 de la directive machine 2006/42/CE - Organismes notifiés
- Article 15 de la directive machine 2006/42/CE - Installation et utilisation des machines
- Article 16 de la directive machine 2006/42/CE - Marquage CE
- Article 17 de la directive machine 2006/42/CE - Marquage non conforme
- Article 18 de la directive machine 2006/42/CE - Confidentialité
- Article 19 de la directive machine 2006/42/CE - Coopération entre les États membres
- Article 20 de la directive machine 2006/42/CE - Voies de recours
- Article 21 de la directive machine 2006/42/CE - Diffusion de l'information
- Article 22 de la directive machine 2006/42/CE - Comité
- Article 23 de la directive machine 2006/42/CE - Sanctions
- Article 24 de la directive machine 2006/42/CE - Modification de la directive 95/16/CE
- Article 25 : Abrogation de la directive machines 2006/42/CE
- Article 26 : Transposition - directive machines 2006/42/CE
- Article 27 : Dérogation - directive machines 2006/42/CE
- Article 28 : Entrée en vigueur - directive machine 2006/42/CE
- Article 29 : Destinataires - directive machine 2006/42/CE
- ANNEXE I de la directive machines - sommaire
- principes généraux - annexe 1 directive machines 2006/42/CE
- 1 EXIGENCES ESSENTIELLES DE SANTE ET DE SECURITE - definitions - Annexe I de la directive machines 2006/42/CE
- Article 1.1.2. Principes d'intégration de la sécurité - Annexe I de la directive machines 2006/42/CE
- Article 1.1.3. Matériaux et produits - Annexe I de la directive machines 2006/42/CE
- Article 1.1.4. Éclairage - Annexe I de la directive machines 2006/42/CE
- Article 1.1.5. Conception de la machine en vue de sa manutention - Annexe I de la directive machines 2006/42/CE
- Article 1.1.6. Ergonomie - Annexe I de la directive machines 2006/42/CE
- Article 1.1.7. Poste de travail - Annexe I de la directive machines 2006/42/CE
- Article 1.1.8. Siège - Annexe I de la directive machines 2006/42/CE
- Article 1.2.1. Sécurité et fiabilité des systèmes de commande - annexe 1 de la directive machines 2006/42/CE
- Article 1.2.2. Organes de service - Annexe I de la directive machines 2006/42/CE
- Article 1.2.2. Organes de service - Annexe I de la directive machines 2006/42/CE
- Article 1.2.3. Mise en marche - Annexe I de la directive machines 2006/42/CE
- Articles 1.2.4. Arrêt, arrêt normal, arrêt d'urgence - Annexe I de la directive machines 2006/42/CE
- Article 1.2.4.4. Ensembles de machines - Annexe I de la directive machines 2006/42/CE
- Article 1.2.5. Sélection des modes de commande ou de fonctionnement - Annexe I de la directive machines 2006/42/CE
- Article 1.2.6. Défaillance de l'alimentation en énergie - Annexe I de la directive machines 2006/42/CE
- Article 1.3. MESURES DE PROTECTION CONTRE LES RISQUES MÉCANIQUES - Annexe I de la directive machines 2006/42/CE
- Article 1.4. CARACTÉRISTIQUES - PROTECTEURS ET DISPOSITIFS DE PROTECTION - Annexe I de la directive machines 2006/42/CE
- Article 1.5. RISQUES DUS À D'AUTRES DANGERS - Annexe I de la directive machines 2006/42/CE
- Article 1.6. ENTRETIEN - Annexe I de la directive machines 2006/42/CE
- Article 1.7. INFORMATION - Annexe I de la directive machines 2006/42/CE
- Article 2. EXIGENCES COMPLÉMENTAIRES POUR CERTAINES CATÉGORIES DE MACHINES - Annexe I de la directive machines 2006/42/CE
- Article 3. EXIGENCES POUR PALLIER LES DANGERS DUS À LA MOBILITÉ DES MACHINES - Annexe I de la directive machines 2006/42/CE
- Article 4. EXIGENCES COMPLÉMENTAIRES - DANGERS DUS AUX OPÉRATIONS DE LEVAGE - Annexe I directive machines 2006/42/CE
- Article 5. EXIGENCES COMPLÉMENTAIRES MACHINES DESTINÉES À DES TRAVAUX SOUTERRAINS - Annexe I de la directive machines 2006/42/CE
- Article 6. EXIGENCES COMPLÉMENTAIRES DANGERS DUS AU LEVAGE DE PERSONNES - Annexe I de la directive machines 2006/42/CE
- Annexe II de la directive machines 2006/42/CE - déclaration CE de conformité
- Annexe III de la directive machines 2006/42/CE - marquage CE
- Annexe IV de la directive machines 2006/42/CE
- Annexe V de la directive machines 2006/42/CE - Liste des composants de sécurité
- Annexe VI de la directive machines 2006/42/CE - Notice d'assemblage d'une quasi-machine
- Annexe VII de la directive machines 2006/42/CE - Dossier technique pour les machines et les quasi-machines
- Annexe VIII directive machines 2006/42/CE - Évaluation de la conformité avec contrôle interne de fabrication d'une machine
- Annexe IX de la directive machines 2006/42/CE - Examen CE de type
- Annexe X de la directive machines 2006/42/CE - Assurance qualité complète
- Annexe XI directive machines 2006/42/CE - Critères minimaux pour la notification des organismes notifiés
- Annexe XII directive machines 2006/42/CE - Tableau de correspondance entre directive machines 2006/42/CE et directive 1998/37/CE
- Directive machines 98/37/CE
- considérants de la directive machines 1998/37/CE
- articles de la directive machines 1998/37/CE
- Annexe I de la directive machines 1998/37/CE
- Annexe II de la directive machines 1998/37/CE
- Annexe III de la directive machines 1998/37/CE
- Annexe IV de la directive machines 1998/37/CE
- Annexe V de la directive machines 1998/37/CE
- Annexe VI de la directive machines 1998/37/CE
- Annexe VII de la directive machines 1998/37/CE
- Annexe VIII de la directive machines 1998/37/CE
- Annexe IX de la directive machines 1998/37/CE
- Directive machines 1989/392/CE
- Considérants de la directive machines 1989/392/CEE
- articles de la directive machines 1989/392/CEE
- Annexe I de la directive machines 1989/392/CEE
- Annexe II de la directive machines 1989/392/CEE
- Annexe III de la directive machines 1989/392/CEE
- Annexe IV de la directive machines 1989/392/CEE
- Annexe V de la directive machines 1989/392/CEE
- Annexe VI de la directive machines 1989/392/CEE
- Annexe VII de la directive machines 1989/392/CEE
- Amendements de la directive machines 1989/392/CEE
- guide de la Direction Générale du Travail modifications de machines
- Directives ATEX
- Directive ATEX 94/9/CE
- Considerants de la directive ATEX 94/9/CE
- Articles de la directive ATEX 94/9/CE
- Article 1 de la directive ATEX 94/9/CE
- Article 2 de la directive ATEX 94/9/CE
- Article 3 de la directive ATEX 94/9/CE
- Article 4 de la directive ATEX 94/9/CE
- Article 5 de la directive ATEX 94/9/CE
- Article 6 de la directive ATEX 94/9/CE
- Article 7 de la directive ATEX 94/9/CE
- Article 8 de la directive ATEX 94/9/CE
- Article 9 de la directive ATEX 94/9/CE
- Article 10 de la directive ATEX 94/9/CE
- Article 11 de la directive ATEX 94/9/CE
- Article 12 de la directive ATEX 94/9/CE
- Article 13 de la directive ATEX 94/9/CE
- Article 14 de la directive ATEX 94/9/CE
- Article 15 de la directive ATEX 94/9/CE
- Article 16 de la directive ATEX 94/9/CE
- ANNEXE I de la directive ATEX 94/9/CE : CRITÈRES DÉTERMINANT LA CLASSIFICATION DES GROUPES D'APPAREILS EN CATeGORIES
- ANNEXE II de la directive ATEX 94/9/CE : EXIGENCES ESSENTIELLES DE SeCURITe ET de SANTE
- ANNEXE III de la directive ATEX 94/9/CE : MODULE: EXAMEN CE DE TYPE
- ANNEXE IV de la directive ATEX 94/9/CE : MODULE: ASSURANCE QUALITE DE PRODUCTION
- ANNEXE V de la directive ATEX 94/9/CE : MODULE VÉRIFICATION SUR PRODUIT
- ANNEXE VI de la directive ATEX 94/9/CE : MODULE CONFORMITE AU TYPE
- ANNEXE VII de la directive ATEX 94/9/CE : MODULE ASSURANCE QUALITE DU PRODUIT
- ANNEXE VIII de la directive ATEX 94/9/CE : MODULE CONTROLE INTERNE DE FABRICATION
- ANNEXE IX de la directive ATEX 94/9/CE : MODULE: VERIFICATION À L'UNITE
- ANNEXE X de la directive ATEX 94/9/CE : marquage CE et contenu de la declaration CE de conformite
- ANNEXE XI de la directive ATEX 94/9/CE: NOTIFICATION DES ORGANISMES
- Directive ATEX 99/92/CE
- Directive ATEX 2014/34/UE
- Considérants de la directive ATEX 2014/34/UE
- les articles de la directive ATEX 2014/34/UE
- Annexe 1 de la directive ATEX 2014/34/UE
- Annexe 2 de la directive ATEX 2014/34/UE
- Annexe 3 de la directive ATEX 2014/34/UE
- Annexe 4 de la directive ATEX 2014/34/UE
- Annexe 5 de la directive ATEX 2014/34/UE
- Annexe 6 de la directive ATEX 2014/34/UE
- Annexe 7 de la directive ATEX 94/9/EC
- Annexe 8 de la directive ATEX 2014/34/UE
- Annexe 9 de la directive ATEX 2014/34/UE
- Annexe 10 de la directive ATEX 2014/34/UE
- Annexe 11 de la directive ATEX 2014/34/UE
- Annexe 12 de la directive ATEX 2014/34/UE
- La nouvelle directive ATEX
- Audits dans le domaine Ex - EN 13980, OD 005 et EN ISO / CEI 80079-34
- La déclaration CE de conformité en ATEX
- Directive ATEX 94/9/CE
- IECEX
- Normalisation & réglementation européenne
- Sécurité des machines - réglementation européenne et normalisation
- Réglementation européenne sur les machines - normes harmonisées
- Sécurité des machines : normalisation et réglementation européenn
- Normalisation dans le secteur des machines
- FD ISO/TR 14121-2 - Février 2008
- ISO 11161:2007
- ISO 13849-1:2006
- ISO 13849-2:2012
- ISO 13850:2006 - Sécurité des machines -- Arrêt d'urgence -- Principes de conception
- ISO 13851:2002 - Sécurité des machines -- Dispositifs de commande bimanuelle -- Aspects fonctionnels et principes de conception
- ISO 13854:1996 - Sécurité des machines -- Écartements minimaux pour prévenir les risques d'écrasement de parties du corps humain
- ISO 13854:1996 Sécurité des machines -- Écartements minimaux pour prévenir les risques d'écrasement de parties du corps humain
- ISO 13855:2010 - Safety of machinery -- Positioning of safeguards with respect to the approach speeds of parts of the human body
- ISO 13856-1:2013 Sécurité des machines -- Dispositifs de protection sensibles à la pression -- Partie 1
- ISO 13856-2:2013 - Sécurité des machines -- Dispositifs de protection sensibles à la pression -- Partie 2: Principes généraux
- ISO 13856-3:2013 Sécurité des machines -- Dispositifs de protection sensibles à la pression - Partie 3
- ISO 13857:2008 Sécurité des machines - Distances de sécurité - zones dangereuses
- ISO 14119:2013- Dispositifs de verrouillage associés à des protecteurs
- ISO 14120:2002 -Protecteurs - Prescriptions generales pour la conception et la construction
- ISO 14122-2:2001 - Moyens d'acces permanents aux machines
- ISO 14122-3:2001- Moyens d'acces permanents aux machines
- ISO 14122-4:2004 - Moyens d'acces permanents aux machines
- ISO 14123-1:1998 - Reduction des risques pour la sante resultant de substances dangereuses emises par des machines
- ISO 14123-2:1998 - Reduction des risques pour la sante resultant de substances dangereuses emises par des machines -- Partie 2
- ISO 14159:2002 - Prescriptions relatives à l'hygiene lors de la conception des machines
- ISO 19353:2005 Securite des machines - Prevention et protection contre l'incendie
- ISO/DTR 22100-2 - Securite des machines - Partie 2: La relation entre l'ISO 12100 et l'ISO 13849
- ISO/TR 14121-2:2012 - Appréciation du risque - Partie 2: Lignes directrices pratiques et exemples
- ISO/TR 18569:2004 - Lignes directrices pour la comprehension et l'utilisation des normes sur la securite des machines
- ISO/TR 23849:2010 - Lignes directrices relatives à l'application de l'ISO 13849-1 et de la CEI 62061
- NF EN ISO 12100 Novembre 2010
- NF EN ISO 12100-1 - Janvier 2004
- NF EN ISO 12100-1/A1 Août 2009
- NF EN ISO 12100-2 JANVIER 2004
- NF EN ISO 12100-2/A1 Août 2009
- NF EN ISO 14121-1 - Novembre 2007
- Liste des normes harmonisées - directive machines 2006/42/CE
- Liste des normes harminisées - directive machines 2006/42/CE - 09.06.2017
- Liste des normes harmonisées - directive machines - OJ C 2016/C173/01 du 15/05/2016
- Liste des normes harmonisées - directive machines 2006/42/CE - corrigendum OJ C 2015/C 087/03 du 13/03/2015
- Liste des normes harmonisées - directive machines - OJ C 2015/C 054/01 du 13/02/2015
- Liste des normes harmonisées - directive machines - OJ C 220 du 11/07/2014
- Liste des normes harmonisées - directive machines - OJ C 110 du 11/04/2014
- Liste des normes harmonisées - directive machines - OJ C 348 du 28/11/2013
- Liste des normes harmonisées directive machines - OJ C 099 du 05/04/2013
- Guide d'application de la directive machines 2006/42/CE, recommendations for use - normes harmonisées
- recommendation for use - directive machines 2006/42/CE
- Organismes notifiés au titre de la directive machines 2006/42/CE
- Sécurité de matériels et équipements EX, IECEx : Normalisation - réglementation européenne
- Normalisation dans le domaine des ATEX et des Ex
- liste des normes harmonisées - directive ATEX 94/9/CE
- Liste des normes harmonisées directive ATEX 2014/34/UE - 12-10-2018
- Harmonized standards list ATEX 94/9/EC directive - OJ C 126 - 08/04/2016
- Liste des normes harmonisées directive ATEX 94/9/CE - OJ C 335 - 09/10/2015
- Liste des normes harmonisées directive ATEX 94/9/CE - OJ-C 445-02 - 12/12/2014
- Liste des normes harmonisées directive ATEX 94/9/CE - OJ-C 076-14/03/2014
- Liste des normes harmonisées - directive ATEX 94/9/CE - OJ-C 319 05/11/2013
- Réglementation européenne pour la directive ATEX 94/9/CE
- Guide d'application de la directive ATEX 94/9/CE
- Guide d'application de la directive ATEX 2014/34/UE
- Alignement de dix directives d’harmonisation technique sur la décision n° 768/2008/CE
- Sécurité des machines - réglementation européenne et normalisation
- Dernières news
- Sécurité fonctionnelle
- Les dispositifs de sécurité en ATEX
- Historique des normes de sécurité fonctionnelle et directive machines
- Sécurité fonctionnelle
- Principes de sécurité éprouvés : l'action mécanique positive
- la sécurité fonctionnelle et les réseaux de terrain
- les microprocesseurs dans les techniques de sécurité
- principes de conception sûr - Les relais de sécurité et les machines
- prévention de la mise en marche intempestive norme EN 1037+A1
- Sécurité fonctionnelle - les codes détecteurs d'erreur - parité et chechsum
- Sécurité fonctionnelle - les codes détecteurs d'erreur - le CRC et les codes de Hamming
- Nouveau règlement machines 2023/1230
Sécurité fonctionnelle - les codes détecteurs d'erreur - parité et chechsum
Les transmissions d'information
Cas de la liaison RS 232 (liaison série)
La RS 232 ou V24 définit deux choses :
- des niveaux électriques (+ 3 Volts à +25 Volts; -3 Volts à -25 Volts)
- une liste de signaux aux fonctions définies
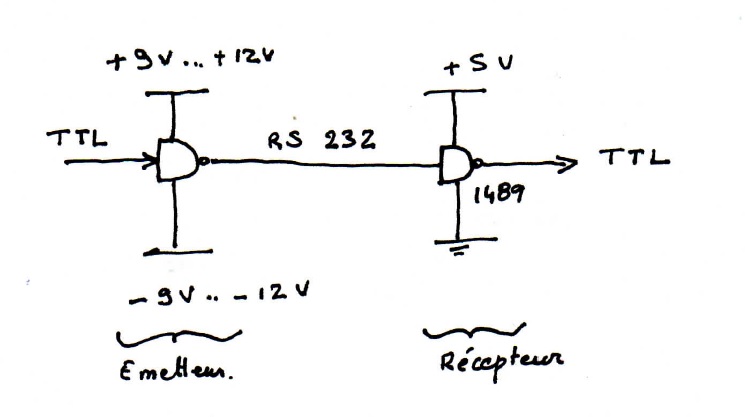
Dans le cas des liasons séries asynchrones, 2 informations sont ajoutées (au repos, le niveau éléctrique / logique de la ligne est à "1").
- avant la transmission : un bit de START (valeur "0"; 1 période)
- après la transmission : bit de STOP (valeur "1"; 1 à 2 périodes)
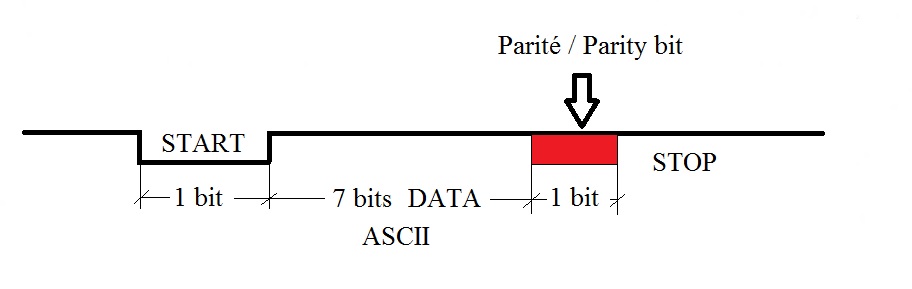
Dans le cas de la transmission des codes ASCII, 7 informations sont nécessaires. A cette information de 7 bit, est ajoutée un bit de parité.
Description de codages détecteurs - correcteurs d’erreurs
La distance de Hamming et le taux d’erreurs résiduelles sont différents pour toutes les méthodes qui permettent de détecter et de corriger ces erreurs de transmission. Les méthodes de codage qui seront présentées dans la première partie de ce document sont :
- Les codes détecteurs d’erreurs par parité,
- Les codes détecteurs d’erreurs CHECKSUM,
- Les codes détecteurs d’erreurs C.R.C.
- Les codes détecteurs et correcteurs d’erreurs par codes de HAMMING
Les deux premières méthodes sont décrites ci-après. Le CRC et les codes détecteurs / correcteurs d'erreurs sont décrits dans un autre article
1. La parité
1.1.Principe de la parité
C'est une somme modulo 2 des bits d'informations. La parité est dite paire lorsque le code de parité est égal à la somme modulo 2 des bits d'informations et impaire lorsque le code de parité est égal au complément de cette somme.
Ce mode de contrôle est utilisé dans les liaisons séries de type RS-232 et dans les microprocesseurs.
Avant chaque transmission d’un mot, un digit supplémentaire est ajouté. Il est appelé bit de parité. Après transmission, la présence d’une erreur simple change la parité et rend l’erreur incriminée détectable.
1.2.Détection d’erreurs - Erreurs résiduelles
Soient « p » la probabilité d’erreur individuelle d’un digit et « n » la longueur du mot.
La probabilité d’avoir une erreur unique est :
P(1) = P[1er digit faux et les (n-1 suivants) justes] + P[1er digit juste 2ème digit faux et les (n-2 suivants) justes] + ...
P(1) = p(1-p)n-1 + (1-p)p(1-p)n-2 + (1-p)2p(1-p)n-2 + ...
P(1) = n[p(1-p)n-1]
De même on obtient :
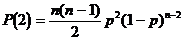
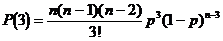
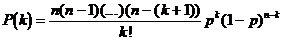
La parité permet de détecter l’ensemble des erreurs impaires d’où un pouvoir de détection PD de :
PD = P(1) + P(3) + ... + P(2k-1)
Les erreurs non détectées sont l’ensemble des erreurs paires d’où un pouvoir de non détection PND de :
PND = P(2) + P(4) + ... + P(2k)
Ces chiffres sont fonction de p, et doivent être calculés en fonction des environnements.
En supposant que nous ayons une trame constituée de 8 bits d'informations et une clé de vérification par bit de parité (n=9). En modifiant un nombre pair de bits e={2, 4, 6, 8} dans la trame nous avons une autre trame dont les erreurs ne seront pas détectées par le contrôle de la clé de vérification.
Le taux d'erreur résiduelle peut être calculé conformément aux éléments fournis en page http://www.industry-finder.fr/la-securite-fonctionnelle-et-les-reseaux-de-terrain.html , et la probabilité d'erreur résiduelle qui en résulte est égale à la somme des erreurs paires soit :
R = R1*R2
avec : R1=P(2)+P(4)+P(6)+P(8) - probabilité d'erreur sur la donnée
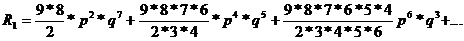
R2 = probabilité pour que les délimiteurs de trame soient juste. Dans le cas de la parité simple, nous avons deux délimiteurs (début et fin de trame) soit une probabilité q * q = q2
Soit :
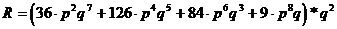
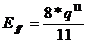
2. Le CHECKSUM
Il existe plusieurs méthodes utilisées pour réaliser un CHECKSUM telles que :
- La méthode de la somme de contrôle modifiée,
- L’addition arithmétique du contenu du message,
- Les codes à parités entrelacées.
C’est cette dernière méthode que nous allons détailler.
2.1.Principe du CHECKSUM
Le principe du CHECKSUM à parités entrelacées consiste en un message de M digits, écrit sous la forme d’un tableau de « L » lignes et « C » colonnes (M = CL). A ce tableau, on ajoute une (L+1)ème ligne et une (C+1)ème colonne construites de telle façon que les mots lus horizontalement et verticalement soient tous pairs.
La méthode consiste à déterminer le nombre de « 1 » contenu dans une ligne (colonne). Si ce nombre est pair, on affecte à l’intersection de cette ligne (colonne) et de la dernière colonne (ligne), l’état « 0 » ou l’état « 1 » si le nombre est impair. Cette opération est effectuée pour chaque ligne et chaque colonne. Le digit placé au croisement de la dernière ligne et de la dernière colonne est choisi pour assurer la parité de l’ensemble du message.
Par exemple, pour un message de M = 49 digits (7 mots de 7 bits):
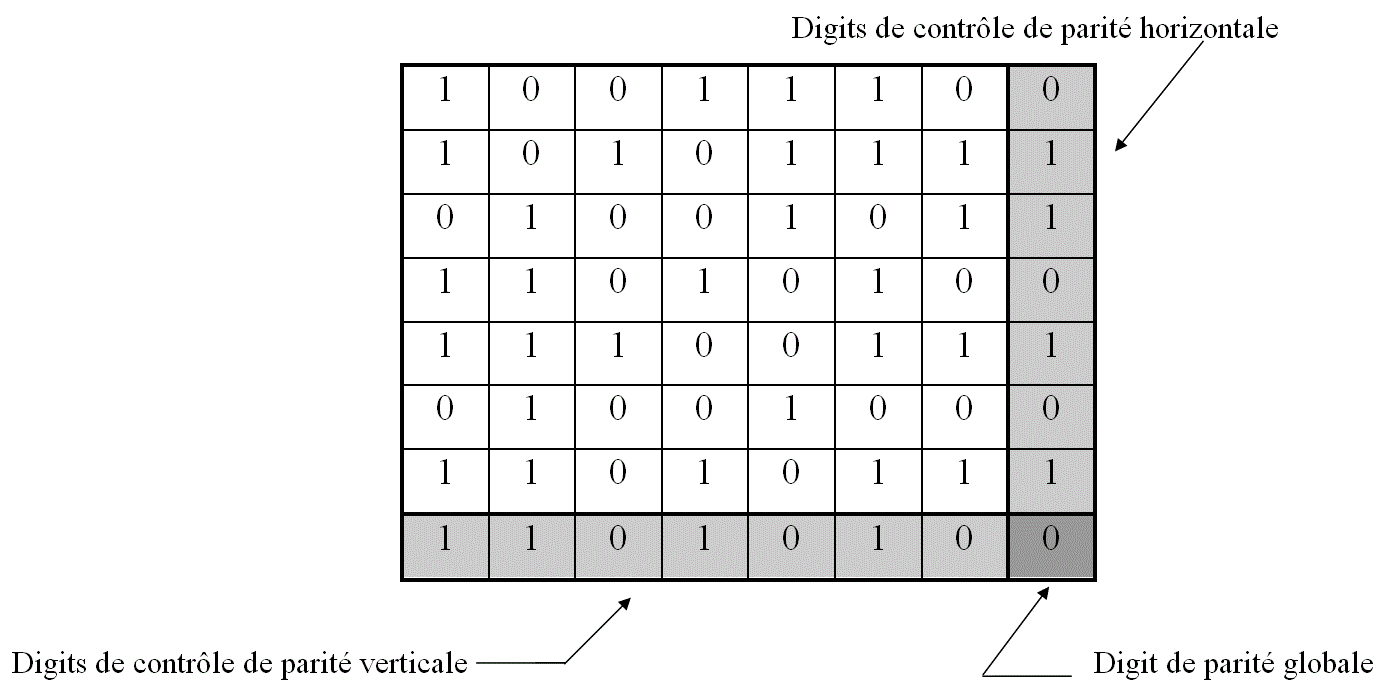
Un ensemble de 64 digits (49 digits transmettant l’information et 15 digits réservés au contrôle) est obtenu et transmis en série dans le canal de transmission. A la réception, le tableau est reconstitué. Une seule erreur fait échouer les contrôle de parité de la ligne et de la colonne correspondante, il y a donc détection et correction possible.
Une erreur double ou quadruple est détectée mais ne peut pas être corrigée, l’erreur triple n’est pas toujours détectée.
Ce code est plus puissant que la parité mais nécessite des ressources matérielles supplémentaires. Un message ayant à l’origine M digits (M = CL) nécessite C + L + 1 digits de contrôle, soit un accroissement de redondances DR de :
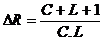
Pour 7 bits d’informations, M = 49 DR = 15/49 = 0.31
Pour 15 bits d’informations, M = 225 DR = 31/225 = 0.14
2.2.Pouvoir de détection du CHECKSUM - Erreurs résiduelles
Le pouvoir de détection du CHECKSUM se calcule de façon différente selon le nombre d’octets, soit à partir d’une méthode principale, soit à partir d’une méthode probabiliste.
2.2.1.Méthode principale
Cette méthode consiste en un dénombrement exact de toutes les combinaisons de « N » mots de « P » bits d’une séquence d’informations conduisant à une somme identique à la somme « S » obtenue sur les « N » mots de la séquence contenant les informations originales.
Le pouvoir de détection théorique PD est défini comme le rapport (exprimé en pourcentage) entre le nombre d’erreurs détectées NDET par le contrôle et le nombre total d’erreurs NTOT pouvant survenir sur la séquence d’informations à contrôler.
L’expression du nombre total d’erreurs NTOT représente le nombre de combinaisons que peuvent prendre les (P x N) bits de la séquence à contrôler, ce qui donne pour N octets:
NTOT = 2P.N
La détermination du nombre NDET ou encore du nombre d’erreurs non détectées NNDET sachant que NDET + NNDET = 2P.N.
NNDET correspond au nombre 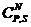 de combinaisons des « N » octets dont la somme est identique à la somme « S » obtenue sur les octets de la séquence d’informations en l’absence d’erreurs.
de combinaisons des « N » octets dont la somme est identique à la somme « S » obtenue sur les octets de la séquence d’informations en l’absence d’erreurs.
Le pouvoir de détection peut alors s’exprimer de la manière suivante :
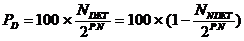
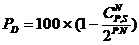
Les calculs réalisant le dénombrement de toutes les combinaisons des « N » octets d’une séquence d’informations dont la somme est « S » conduisent aux formules suivantes :
pour S = 0 ; 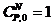 ; P = 8 bits (Nombre de bits dans un octet)
; P = 8 bits (Nombre de bits dans un octet)
PD = 100 x (1-1/28.N) » 100 %
Pour S 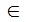 [ k (2P - 1),(k+1) (2P - 1)] avec k entier
[ k (2P - 1),(k+1) (2P - 1)] avec k entier 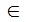 [ 0 , N-1-INT(N/2P)]
[ 0 , N-1-INT(N/2P)]
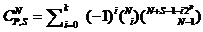 0! = 1
0! = 1
ou 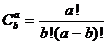
Le calcul numérique n’est possible que pour de petites valeurs de N (N < 40). Au-delà de ce niveau, il faut avoir recours à la méthode « probabiliste ».
2.2.2.« Méthode probabiliste »
Avec la « méthode probabiliste », chaque octet peut être considéré comme une variable aléatoire. Une configuration donnée étant la séquence des « N » variables aléatoires correspondantes.
Si l’on considère que la loi de distribution est la même pour chaque octet, (moyenne m, variance s2), lorsque « N » est grand (N>50), la distribution de la somme « S » des variables aléatoires est très sensiblement normale, de moyenne Nm et de variance Ns2, d’où la probabilité que la somme des « N » variables soit égale à une valeur « s » :
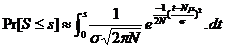
La probabilité d’une valeur « s » entière est donc :
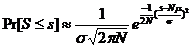
avec 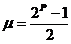 et
et 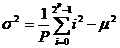
La probabilité est maximale pour la valeur Nm de « s » :
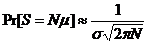
Appliquée à des mémoires de données de taille 8 bits (P = 8) et de capacité donnée, nous obtenons les résultats suivants :
Pour P = 8
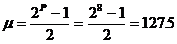 et
et 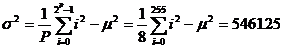
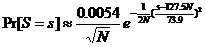 et
et 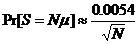
Pour :
N = 512 o Pr[ S = 65280 ] ~ 0.0002386 (99.976 %)
N = 16 ko Pr[ S = 2088960 ] ~ 0.000042 (99.9958 %)
N = 1 ko Pr[ S = 130560 ] ~ 0.0001688 (99.983 %)
N = 32 ko Pr[ S = 4177920 ] ~ 0.0000298 (99.997 %)
French
